Slot Machine
Payback Percentages:
The Devil
is in
the
Moment
Scott Farrow and Jackson Costa UMBC - Working Paper November 24, 2013
Corresponding author:
Scott Farrow
Department of Economics UMBC
1000 Hilltop Circle Baltimore, MD, USA 21250
Tel. 410-455-5922
e-mail:
farrow@umbc.edu
Acknowledgments:
The authors thank the Maryland Lottery and Gaming Control Agency for
data and for reviewing preliminary findings and Gambling Laboratories
International for communication on industry practice.
We thank the John D. and Catherine T. MacArthur Foundation for
providing research support to Costa.
Tim Brennan, Tim Gindling, Jay Kadane, Nagaraj Neerchal and Andrew
Solow provided comments
on an
earlier draft
but any
errors remain
the responsibility of
the authors.
Comments are welcome to
Farrow@umbc.edu .
Abstract
The average payback percentage from slot machines is important to gamblers, casinos, and governments. While apparently simple to define several complications can exist, among them which measure to average and potentially misleading formulas to calculate the average. Daily slot machine data from the state of Maryland for 19 months are analyzed for the expected value of the average payback ratio per machine and per dollar gambled. On a per dollar gambled basis, the payback percentage meets legislative requirements that the gaming floor payback at least 90 percent. On a per machine basis, that requirement is not met which can imply a significant shift of money from gamblers to casino operators and the state. Other payback measures are hypothesized to also be less than the per-dollar gambled measure but data are lacking.
Introduction
Payback percentages are important features of casino advertising, reporting, and legislation. Gamblers are believed to seek locations where the payback percentage is large. Informally, advertising boasts of “loose slots”. Legislators may specify payback percentages for various reasons, such as its effect on government revenues, consideration of competition, and consumer response. Computing the payback percentage, the ratio of “total coin in versus total coin out” as stated by one casino manager, may seem simple but there subtleties to correctly defining and calculating the mean, the first moment, of a ratio1. Differences in definition and calculation can swing the result by several percentage points, a substantial financial change to the various stakeholders and one which can have legal implications.
The importance of alternative methods of calculation is investigated using data for all slot machines in the state of Maryland in the United States over 19 months from 2010 to mid-2012. Differences in the definition of average payback percentage can change the result by about 3 percentage points, enough in Maryland to move the estimated payback ratio from out of compliance to in compliance. The policy implication is that legislators or regulators should carefully define what they intend as a payback percentage as the measure has important monetary implications for the distribution of gambling revenues.
The paper proceeds by presenting legislative requirements for payback percentages specific to the state of Maryland, the expectation of a ratio such as payback ratio, alternative definitions of what is to be averaged, a description of the data, results, and the results from a re-test using alternative and different data provided by MLGCA. The paper concludes with observations for regulators and legislators on alternative ways to define payback percentages.
Payback ratios: legislative requirements
Many states and jurisdictions require minimum payout percentages and some report payback percentages, among them Connecticut, Louisiana, Nevada and New Jersey. Maryland’s original legislation legalizing slot machines specified criteria for the payback percentage to gamblers as well as revenue shares of gross terminal revenue (GTR) between the state and operator (Maryland Senate 2007). Regulations, with the legal force of law, are often written after legislation has passed in order to further define policy. Such is
the case here with regulations being developed after the legislation and promulgated in the Code of Maryland Regulations (COMAR) and overseen by the Maryland Lottery and Gaming Control Agency (MLGCA).
![]()
1
Which
when multiplied
by 100
yields the
payback
percentage.
The primary legislative criteria investigated here is whether a facility’s average payback is between 90 and 95 percent and the individual slots achieve an average payout ratio of 87% per machine. The American Casino Guide (2013) reports that “no public information is available about the actual payback percentages on gaming machines in Maryland”. Communication with the MLGCA indicated that while they did not have the payback percentage available, such numbers are required to be displayed at each casino in the state2. Consequently this paper utilizes machine specific payback data to investigate issues in the definition and quantification of payback ratios and their consistency with Maryland law and regulation.
Legislative and regulatory definitions of payback ratio
Maryland legislation defines the payback percentage in terms of an average percent: “Average payout percentage means the average percentage of money used by players to play a video lottery terminal that is returned to players of that video lottery terminal” (Maryland Senate 2007). This definition appears to be the average of the payout ratio, the expectation of a ratio while leaving the nature of the observational average ambiguous; whether per machine, per bet, per dollar or something else. The legislation then continues to define required payout percentages in terms of the average payout percentage at each facility
Later, regulations elaborated on the legislation.
Maryland regulations in force during the period of the data defined a
new term, the “theoretical payout percentage”, as “the total value of
jackpots expected to be paid by
a video lottery terminal divided
by the total value of video
lottery terminal wagers expected
to be made on that video lottery terminal during the game cycle3”
(Code of Maryland Regulations (COMAR), 14.01.15).
This definition can be interpreted as a computation of the expected
value (average) of
the amount
paid per
machine divided
by the
expected value
(average) of
the amount
wagered per machine; the ratio of expected values because the number
of observations in the numerator and denominator would cancel each other.
This will be shown to be a correct estimator under one definition of
“average” and an incorrect definition under another.
However, the operational test and title of the regulatory section in enabling legislation referred to the “average payout percentage”. Further, the legislative requirement that the average payout percentage be achieved at each facility is changed in regulation to be “A facility’s gaming floor shall be configured to collectively achieve, at all times, an average payout percentage…” and that periodic evaluations occur to determine that “average payout percentages, on an average annual basis, comply with the requirements of this regulation.” (COMAR, 14.01.11B-F
The regulatory criteria then combine elements of both the theoretical payback percentage and the average payback percentage as below (italics added, COMAR 14.01.11B-F):
B. A video lottery terminal shall have an average payout percentage which:
(1) Is 87% or more; and
(2) Does not exceed 100%.
2 The payback values were not located during one casino site visit but both the MLGCA and the site later provided information indicating the payback percentage for the preceding three months.
3 “Game cycle” is also defined as the “finite set of all possible combinations”.
E. A facility’s gaming floor shall be configured to collectively achieve, at all times, an average payout percentage which:
(1) Exceeds 90%; and
(2) Does not exceed 95%.
G. Once a facility is operational, the Commission shall:
(1) Conduct periodic reviews to ensure that average payout percentages, on an average annual basis, comply with the requirements of this regulation;
This paper focuses on requirement E and G and alternative definitions of the payback ratio although necessarily aggregating across several sites as the specific machine location is unknown. Information on individual machines as specified in requirement B is also investigated.
Average Payback as the Expectation of a Ratio
The measure of “average” most typically used is the expected value of random variable, E(X). For discrete data such as occur with gambling, the observations Xi are weighted by the probability of their occurring, πi , and then summed.
![]()
E(X) = ∑
In the case of a payout ratio, X is defined as P/W where P is the amount paid out and W is the amount wagered4. The familiar sample average occurs when πi is 1/N. When some aggregation occurs, as with amounts paid and wagered for each machine, the probability incorporates the aggregation process which is one reason πi can vary by observation.
A potential pitfall in estimation of the average of the ratio, P/W, is that the expectation of the ratio does not in general equal the ratio of the expectations (e.g. Heijmans 1999; Mood, Graybill and Boes, 1974). A brief investigation of this issue reveals an important connection between estimation of an average payback ratio per machine and per dollar.
The relation between the mathematical expectation of a ratio and the ratio of expectations can be stated in terms of the covariance between P/W and W and is defined as5:
COV(P/W,W)
=E(P/W*W)-E(P/W)E(W)
Setting this equation equal zero implies that E(P/W) equals E(P)/E(W) only when that covariance is zero; the expectation of the ratio will equal the ratio of expectations only under a restrictive condition. Further, if the covariance is positive, then the ratio of the expectations, E(P)/E(W), is greater than the expectation of the ratio, E(P/W). If in fact there is a positive covariance between the ratio and the amount paid in, then the ratio of the two expectations will exceed the actual expectation of the ratio.
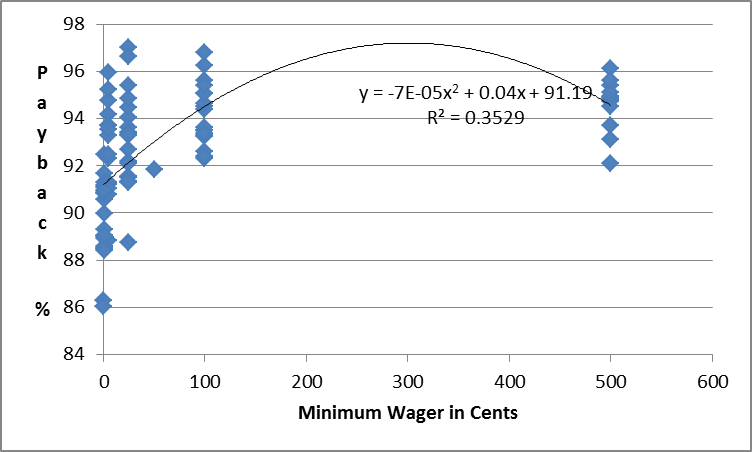
Reports on slot paybacks indicate that higher payback ratios tend to be associated with higher wager machines in which case the expected value of the ratio would be less than the ratio of expectations. For instance Figure 1 plots recently reported payback ratios in six states6. While a fairly broad range in each betting category can be observed, so too can a upward trend from the lowest bet slots to the $1 level at which point the payoff ratio appears to level off. A least squares second order polynomial fit to the data supports the visual interpretation, implying a hypothetical maximum payback between the $1 and $5 bets.
4 What constitutes Paid and Wagered can still have accounting complications, such as the treatment of promotional funds.
5 This variation on the standard covariance definition is found in many sources such as Mood, Graybill and Boes (1974, p.156).
Procedure in the state of Maryland and presented as the industry standard is to compute the payback ratio as E(P)/E(W). It will be demonstrated that this choice of computing the payback ratio is correct when the average payback per dollar is the measure of choice but incorrect, and expected to overstate the true value, if the average payback per machine is the measure of choice.
Alternative Payback Averages: Defining the Units of Measurement
The data to be analyzed were provided for each slot machine for each day. A test for compliance for regulation thus requires interpreting the specific variable to be averaged. On the basis of legislation alone, the average is to consider a ratio of money repaid at each lottery terminal. Regulatory language doesn’t improve on the clarity by adding words such as “gaming floor” and “collectively achieve” in the material cited above7.
One potential “average” measure is thus the average payback per machine on the gaming floor where the average is the usual sample average using the number of machines as the weight. This average is useful as a baseline as different measures ultimately associate different probabilities with the machine data as summarized in Table 1 and discussed below.
6 The six states are Colorado, Connecticut, Nevada, Louisiana, Mississippi, and South Dakota. The computation of payback percentages is not clearly defined but speculated to be on a per dollar gambled. The data may be for each state or for sub-regions (American Casino Guide 2013).
7 Other states may or may not have similar ambiguity. Maine (2013)defines the average payback percentage in similarly vague terms. Nevada (2013) is more precise when defining a theoretical hold percentage in footnotes as being based on a weighted average.
A second potential measure is average payback per dollar wagered which
probability weights each machine
by its
share of
total wagers.
Thus machines
with larger
dollar amounts
wagered, whether
through higher betting
limits, more
frequency of
play, or
a combination
of the
two will
have a
larger impact
on the average than would
a machine with a lessor amount wagered.
Consistent with this observation, in Maryland, it has been stated
that “VLTs with higher wagering limits typically have higher payback
percentages and tend to generate a significant higher portion of the
facilities revenues” (MLGCA 2013).
As shown in Table 1, the expected payback per dollar value is correctly measured as the ratio of expectations of the amount paid in per machine and the amount wagered per machine when each machine is probability weighted by its share of wagers. This estimate of the payback ratio, if a positive covariance exists between the amounts wagered and the payback percentage, will be larger than the expected value of the ratio on a per machine basis.
Table 1 Alternative measures of the average (expected value) payback ratio
Measure
Probability Weight For Machine Based Data
Alternative Values E(P/W)
Comments and Hypotheses
Per Machine
1/N; N = machines
μ = ∑
N
Per Dollar
1/W; W= Total Wagers
μ ∑
D =
∑
If higher payback
Wagered
Machine weight Wi/W where Wi
machines have higher
wagers per machine
share of wagers,
μD > μN
Correct per dollar ratio
equals incorrect per
machine calculation
Per Bet
1/B; B= Total Bets Machine weight Bi/B where Bi bets
per machine
μ ∑
B =
∑
If lower payback machines have higher
share of bets, μB < μN
Per Gambler
1/G; G= Total Gamblers Note: G < ΣGi due to wagering on
multiple machines8.
μG
If lower payback machines have higher share of gamblers,
μG < μN
A third potential measure is the individual bet payoff ratio which forms the most micro basis for calculation. The payback ratio could be averaged over all bets for the time period to obtain an average payback per bet. A large proportion would have zero payback. Given computer capabilities, such storage and calculation appears possible but was not discernible in the data provided. The impact on the average payback ratio is uncertain but to the extent that more bets are placed on smaller denomination machines with lower payback ratios, then the average payback per bet would likely be less than the average payback per machine and per dollar spent. This measure is not computable with the data available.
The fourth and final measure considered is the average payback per gambler. This measure encompasses each gambler’s choice of the number of bets, which machines, how much to wager, and when to exit.
Such an average is likely measurable for members of casino loyalty reward programs where their presence on a machine is recorded. It would be more difficult to identify the average payback to individual gamblers who are not part of loyalty reward programs due to difficulty in determining when one gambler stops and another begins on a machine and also when a gambler changes machines. In general, the number of gamblers at a site will be less than the sum of gamblers on machines due to some gamblers playing on multiple machines. To the extent that more gamblers play lower wager slot machines than higher wager, higher payback slot machines, it is possible that the average payback computed in this way would be less than the average per machine. This measure is not computable with the data available.
8 Machine weight undefined without allocation of gamblers across machines.
Data
Individual slot machine data by day were obtained from the Maryland Lottery and Gaming Control Agency (MLGCA). Following a Freedom of Information Act request, the MLGCA provided data consisting of slot machine (video lottery terminal) information in the state of Maryland from September 27th, 2010 to May 1st, 2012. The data contained information for each slot for each day it was in use. The content of the original data are reviewed in detail in the Appendix as the agency later provided an alternative dataset. The alternative dataset, described later, leads to the same qualitative and almost exactly the same quantitative results and so the original data are used here.
Variables provided in the data set are:
· Date associated with collection of data
· Slot identification number (ID)
· Cash played gamblers on the given date and slot
· Cash won by the gambler on the given date and slot
· Promotional cash played (Promo) by the gambler on the given date and slot
· Gross terminal revenue (GTR), which is defined in the data provided as the cash played minus the sum of promotional cash played and cash won.
· Time data was collected for given day (8:00 AM for each entry)
After formatting and editing the data as described in the Appendix, 1,278,327 observations remained for the entire time period, a change of 13,654 observations from the original data; the vast majority of which were due to formatting such as deleting blank lines or lines that summed the total for a day
Descriptive Statistics
Descriptive statistics for the cleaned data are presented in Table 1. The average Cash Played is somewhat over two thousand dollars per day at $2,119 and Cash Won is somewhat less than two thousand at $1,921. The average Promotional Cash is $8 per machine per day with standard errors of a few dollars and standard deviations (not in table) the same order of magnitude as the means. The minimum for each item is zero9 while the maximum won in day was a little over $235 thousand.
Computing payback percentage depends on one further definition involving promotional cash. In the data provided by MLGCA, the amount paid to a gambler appeared to be defined as the sum of cash won by the gambler plus the promotional cash played by the gambler, as if the gambler “won” the promotional cash provided by the casino operator. The numerator in the base payback percentage calculation includes cash paid to the gambler and the cash equivalent given to the gambler to encourage gambling. This sum of cash played and promotional cash and is labeled below as “Paid” or P. The denominator, which is labeled “Cash Played” or wagered (W), is the amount of cash input into the machine by the gambler. Alternative treatment of the promotional cash, such as deleting it from the numerator or adding it to the denominator would only decrease the payback ratios reported here.
9 In order to analyze payout ratios described later which use logarithms (where the logarithm of 0 is undefined), one cent was added to cash played if the actual cash played was zero.
Table 1:
Descriptive Statistics
of the
Cleaned data
(truncated to
dollars)
|
|
N |
Mean ($) |
Std. Error ($) |
Min. ($) |
Max. ($) |
|
Cleaned Data |
|||||
|
Cash Played |
1,278,327 |
2,119 |
2.61 |
0 |
211,959 |
|
Cash Won |
1,278,327 |
1,921 |
2.52 |
0 |
235,539 |
|
Promotional Cash Played |
1,278,327 |
8 |
.02 |
0 |
3,133 |
Results: Analysis of data averages
Averages across years and operators
The results of estimating the payback ratio using the two different methods are presented in Table 2 along with other descriptive data and discussed below.
Table 2: Alternative Measures and Methods to Calculate the Payback Ratio
|
Method |
Formula |
Result |
Std. Error |
N |
|
Average per machine |
|
μN = .881 |
.0003 |
1,278,327 |
|
Average per dollar spent |
|
μD = .910 |
N.A. |
1,278,327 |
Results using the average per machine are presented in row 1. This expectation for the entire data set is 0.881, less than the legislative minimum of 0.90. Taking uncertainty into account, the 95% confidence interval for the mean of P/W is small10, ranging from 0.88 to .882. The confidence interval does not include the legislation minimum requirement of 0.90.
Results using the average per dollar wagered are presented in row 2. This expectation for the entire data set is 0.91, greater than the legislative minimum of 0.90. From Table 1 above, the computational formula uses the average Wagered per machine and the average value Paid per machine can be computed as the sum of the averages of Cash Won plus Promo Cash. Taking the ratio of these two averages yields a payout percentage per dollar that which meets legislation requirements and is higher than the payback ratio per machine.
Note that
that the
correct formula
for the
average payback
ratio per
dollar can
be expressed
as the
ratio of the expectations
per machine of the two components.
On the basis of these results, the conclusion is that the
observed average payback percentage is in compliance
with legislation
if the
average per
dollar wagered
is used
as the
compliance measure
but out of compliance if
the average per machine is the compliance measure.
10 Note that the confidence interval of the mean is constructed using the standard error which is the standard deviation divided by the square root of the number of observations.
Implications
for the
distribution of
gaming
revenues
The choice of how to compute the payback percentage can have measurable implications for the amount of money retained by gamblers and that received by casinos operators and the government. That difference is illustrated in two ways. One computation is based on bringing the payback ratio per machine up to the level of the payback ratio per dollar, a difference here rounded to three percentage points. A second computation, the change necessary to achieve the legislatively required minimum for the gaming floor, is here rounded to two percentage points. The shift in revenue from gamblers to the state and casinos during the 19 months studied would be approximately 134 million dollars in the former case and 89 million dollars in the latter case.
Average
across
machines
Regulation and legislation also contains a requirement for individual machines. Analyzing data at the single machine level, 900 out of 2,473 unique machines have average daily payouts that are below the legislation requirements of .87. When the average per dollar wagered is used, 170 machines were below the legislation requirement. Of the 2,473 machines, 48 of the machines had average cash played less than
$100. This suggests that these particular machines may be new or in a location that limits the use of the machines. From these 48 machines, 40 of them do not meet the legislation requirement with either of the definitions for payout. There is nothing unique about the $100 threshold used; machines are anticipated to have observed payback percentages closer (in the sense of a smaller confidence interval) to their population expected value when the number of plays is larger.
Machines may also exceed allowable payback percentages and similar cautions about small levels of play exist. In all, 49 machines had payback percentages calculated in either way which exceeded the legislative maximum of 95 percent. Such exceedances can be approved by the Commission regulating slots (Maryland Senate, 2007).
Alternative results using regression analysis
The preceding section used sample averages to evaluate consistency with legislation. Regression analysis can also be used to test hypotheses about consistency with legislation and also relax the assumption of a constant payback ratio.
Define the payback ratio as α:
For ratio formulas of this kind, it is common to apply a logarithmic transformation such that:
The unweighted regression to be estimated is defined
below where the coefficient preceding the wager term
is β
and a
standard error
term, ε,
assumed to
be normally
distributed with
mean zero
and a
variance is added:
Given the legislative requirements, it is expected that the entire data set would satisfy or when transformed into logarithmic values,......................................... If the payback percentage is constant, then is expected to equal 1. For individual machines, it is expected that where i indicates an individual machine. The hypothesis tests reported here focus on the minimum that is legislatively required based on the results of the sample averages reported above11. The analysis per machine is based on a regression using unweighted data consistent with a per machine analysis.
Hypothesis tests for the consistency of the data with legislative requirements were then conducted as follows:
1. β = 1
2. Intercept = ln .9 = -.105
Regression results
The results of the ordinary least squares regression analysis are presented in Table 4. The data fit the regression well with an R2 of .95. The intercept and slope coefficient are highly significant, as might be expected with over 1 million observations. Given the small standard errors and that neither coefficient is in the close neighborhood of the values to be tested, it would be expected that formal hypothesis tests would reject consistency with regulatory requirements which is correct; similarly for a joint test of the hypotheses. Consequently the data reject consistency with legislative requirements for this regression per machine and also that the payback ratio is uncorrelated with the amount wagered.
Table 4: Regression test of consistency with legislative requirements Dependent variable: Ln(Paid); per machine
* ”P” value < .001; standard errors in parentheses
Further insight into the payback ratio can be inferred from the coefficient on the logarithm of the amount wagered. That coefficient has an interpretation as an elasticity, the percentage change in the dependent variable per one percent change in the independent variable. The elasticity of the amount paid with respect to the amount wagered is 1.08 indicating a 1.08 percent increase in the amount paid for each one percent increase in the amount wagered. This is consistent with some publicly available information on slot machine design suggesting that the payback percentage can increase with the amount wagered on each play and with some progressive types of betting. It is also evidence that the covariance between Paid and Wagered is non-zero and positive.
Alternative data and alternative formulas
The preliminary results, focusing on different methods of calculating the average per machine, were provided for comment to the MLGCA in 2013 who responded in essence that different data should have been provided for a payback ratio analysis. In September of 2013, the MLGCA provided “adjusted” data. Several data anomalies remained such as several negative values for cash played which were deleted.
The payback ratio were recomputed with the adjusted data with the results presented in Table 5. As the mean data are consistent and almost identical to that obtained using the original data above, no changes were deemed necessary to the above analysis.
11 In addition, as it is possible for the amount paid to be zero for a machine. As the logarithm of 0 is undefined, one cent (.01) was added to the raw data if amount paid was zero (wagered was required to be positive for inclusion).
Table 5:
Payback ratios
with original
and adjusted
data
|
Method |
Result |
|
|
Original data |
||
|
Payback per machine |
.881 |
|
|
Payback per dollar |
.910 |
|
|
Adjusted Data |
||
|
Payback per machine |
2010 |
.88 |
|
|
2011 |
.88 |
|
|
2012 |
.88 |
|
Payback per dollar |
2010 |
.91 |
|
|
2011 |
.91 |
|
|
2012 |
.91 |
During the exchange of results on the adjusted data with the MLGCA, the MLGCA noted that they calculate the payback ratio as Won/Played including an explanation that promotional cash cannot be cashed out as winnings but is counted in the amount played. Alternatively, a later communication from the manager of Maryland casino defined the payback percentage as “total coin in versus total coin out”. If “coin out” is interpreted as “Won” and “coin in” as Played less Promotional, then another alternative formula could result defined as Won/(Played-Promo). In essence, each of these alternative formulas places the promotional cash in different parts of the formula. As it can be shown that the measure used above, (Won+Promo)/Played, is larger than both Won/Played and Won/(Played-Promo) then results presented above understate the divergence in payback ratios12. However, as the value of the promotional amount is small, the quantitative difference might also be expected to be small which is confirmed in Table 6 using the adjusted data for year 2010. Consequently no changes have been made to the analysis in the preceding sections. This additional area of ambiguity about the numerator and denominator is an additional indication of the care which should be devoted to definitional issues affecting the distribution of funds.
Table 6: Alternative Payback Ratio Definitions with adjusted data
|
Year |
E(Won+Promo)/Played Per machine |
E(Won/Played) Per machine |
E(Won/(Played-Promo) Per machine |
|
2010 |
.8802 |
.8743 |
.8797 |
Conclusion
The average payback percentage appears to be important to gamblers, casinos, and government. While apparently simple to define, two key issues exist for the design and oversight of gambling. The first is understanding the implications of what average is to be used to define the payback ratio. Is it per machine? Per dollar wagered? Per gamble? Some measures can be expected to be larger than others given likely configurations at gambling sites. Second, analysts may consider using different computational formulas for the average. It is demonstrated here that the expectation of the ratio, the apparent correct measure, has a simplified form when the average per dollar wagered is the desired measure. However, that simplified form, the ratio of the expectations, would be an incorrect measure of the per machine payback ratio.
Using two sets of data provided by the MLGCA, the operational values for average payback ratios are found to be inconsistent with legislation if the average per machine is used. In contrast, the payback ratio is consistent with legislation if the average payback per dollar wagered is used. This result is found to be invariant to the data set used or minor variations in the accounting definition of the payback ratio. The difference in payback ratios is potentially significant for the compliance purposes and financial impact.
The results suggest care by legislators and oversight agencies in the definition of what appear to be small details such as the formula of the average payback ratio. In addition, this research suggests the usefulness of detailed publicly available data both at the somewhat aggregated level used in this study, each machine by day, and also for more finely detailed on individual gambles available to casino operators but generally not to regulators or the public. The availability of such data may improve our understanding of both basic attitudes toward risk, the context of gambling, and the design of the gambling environment.
12 The latter inequality holds as long as “coin in” exceeds “coin out” which is clearly true for the data in aggregate.
References
American Casino Guide, Slot Machine Payback Statistics, available at http://www.americancasinoguide.com/slot-machine-payback-statistics.html; accessed April 28, 2013
Barnett, V. and T. Lewis ‘Outliers in Statistical Data’ (John Wiley & Sons, 2d ed., New York, NY, 1985) Code of Maryland Regulations ‘Video Lottery Technical Standards’ and related sections, (COMAR
14.01.11B-F; 14.01.15; 14.01.22A) accessed March 28, 2012.
Dean, R. B. and W. J. Dixon ‘Simplified Statistics for Small Numbers of Observations’ (1951) 23:4 Anal.
Chem. 636–638
Heijmans, R. ‘When Does the Expectation of a Ratio Equal the Ratio of Expectations?’ (1999) 40
Statistical Papers 107-11
Maine, Maine Revised Statute, MRS Title 8, Chapter 31: Gambling Control Board, 1:1001(34), available at www.mainelegislature.org/legis/statutes/8/title8 (2013).
Maryland Senate Senate Bill 3: Maryland Educational Trust Fund: Video Lottery Terminals (2007) accessed April 28, 2013.
MLGCA, Email from Charles LaBoy, Assistant Director for Gaming, October, 31, 2013.
Mood, A., F. Graybill and D. Boes Introduction to the Theory of Statistics. (New York, McGraw-Hill Publishing Company, 3rd ed., 1974)
Nevada, Gaming Statues and Regulations, Technical Standards for Gaming Devices and Associated Equipment, Standard 3 (see notes, page 2 and 3), available at http://gaming.nv.gov/index.aspx?page=51 (2013)
Appendix:
Formatting and
cleaning original
data
The original data set was provided in three Excel data files that required additional formatting and editing prior to its use in the software chosen for its ability to handle large datasets, the Statistical Analysis System (SAS) software. The formatting issues involved:
1. Filling in the date for observations in sequence where it had not been explicitly written
2. Deleting rows that contained daily cumulative totals over all machines
3. Deleting rows that were used as gaps between dates
4. Deleting rows with zeros for all data
5. Deleting rows with no ID numbers for a machine
6. Removing time from date column as all data were reported as collected at the same time
7. Providing variable column names for headers to be used in SAS
Data modification to clean the data
Following an initial review of the formatted data, it was noticed that some observations showed over a million dollars being bet during a day and other values that seemed unlikely. The MLGCA was contacted in regard to these possible anomalies. Relatively general guidance was provided in reply and is copied below:
· The “*” represents no game play.
· The only time you will see negative amounts in the cash played, won, etc… is when there was a slot issue or configuration issue. These types of anomalies are adjusted for during the invoicing process.
· Large numbers as you identified are a result of slot or configuration issues. Again, these types of anomalies are adjusted for during the invoicing process.
· My suggestion is that you eliminate the anomalies from your analysis. The anomalies are easily explained per occurrence as we will investigate it on the day it occurred.
Consequently, the following changes in addition to formatting and editing were made to the data provided by MLGCA:
1. Deleted observations with “*”, negative cash played, negative cash won, and negative promo cash
2. Deleted observations that contained values of 1 million or more
3. Evaluated nearest neighbor data points for changes in gross terminal revenue as informed by but not restricted by usual assumptions of a small data set and normality (e.g. Barnett and Lewis, 1985; Dean and Dixon, 1951). Large gaps are thought to represent outliers although the small probability but large payback format of slot machines suggests that large gaps are possible. Four observations were deleted which were not already deleted by the above rules.